The Fibonacci series is a mathematical sequence of numbers named after Italian mathematician Leonardo Fibonacci. Each number is the sum of the two preceding numbers (Fibonacci recursion, fib recursion). This sequence begins with 0, 1, 1, 2, 3, 5, 8, etc. (Fibonacci number).
| Post Type: | Java Programs Examples |
| Published On: | www.softwaretestingo.com |
| Applicable For: | Freshers & Experience |
| Get Updates: | Join Our Telegram Group |
Beyond its mathematical significance, the Fibonacci series has intriguing connections to nature, particularly in the concept of the golden ratio. This ratio, derived from the Fibonacci sequence, appears in diverse natural phenomena, highlighting the series’ presence in the world around us.
The Fibonacci series is a basis for solving problems and modeling natural processes in real-life applications. As we delve into its definition and properties, we uncover its relevance in fields ranging from mathematics to biology.
In summary, with its recursive definition and inherent connection to the golden ratio, the Fibonacci series transcends the realm of mathematics, impacting both theoretical and practical aspects of various disciplines.
What Is The Fibonacci Sequence Series Or Number In Java?
The Fibonacci series is a sequence of numbers that builds upon itself, with each number being the sum of the previous two numbers. The first two terms are ‘0’ and ‘1’. The term ‘0’ might be omitted in some older series versions.
So the Fibonacci series numbers can be like 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, etc, if you observe that every term can be calculated by adding the two terms before.
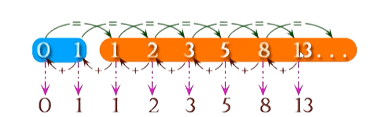
Fibonacci Sequence Recursive Formula
The Fibonacci sequence follows the recursive formula: f(n) = f(n-1) + f(n-2). For example, the 2nd Fibonacci number is 1; the third is 1; the fourth is 2 (1+1); the fifth is 3 (1+2); the sixth is 5 (2+3), etc. (recursive fib, fib recursion, Fibonacci sequence recursive formula, Fibonacci recursion, Fibonacci recursive). The sequence can be calculated recursively by taking the sum of the prior two numbers (recursion).
The Fibonacci sequence begins 0, 1, 1, 2, 3, 5, 8, 13… (fibonaci series, serie fibonacci, fibonacci def). Though discovered mainly out of mathematical curiosity, Fibonacci numbers are relevant in many fields, including computer science and even art (series meaning).
To find the nth term in the Fibonacci sequence, you can use the below formula:
Fn = Fn-1 + Fn-2, where n > 1
Fibonacci Series Spiral
The Fibonacci numbers emerge in nature from the spiral arrangement of leaves to the shapes of seashells and pinecones (Fibonacci nature, Fibonacci series, and Nature). Each number is approximately 1.618 times greater than the preceding (golden ratio Fibonacci series). This ratio is called the Golden Ratio, and it often appears in geometry and nature.
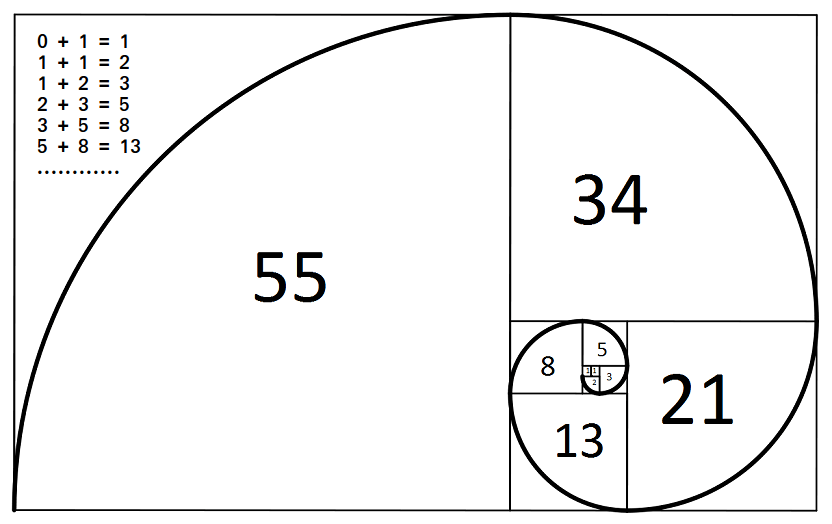
Here is an image of a Fibonacci spiral. This type of spiral is created by partitioning a rectangle into 2 squares. The Fibonacci spiral is an approximation of the golden spiral.
Fibonacci Series List
The Fibonacci Series List is a series of numbers in which each term is the sum of the two preceding terms. The first 20th Fibonacci numbers are given below.
| F0 = 0 | F10 = 55 |
| F1 = 1 | F11 = 89 |
| F2 = 1 | F12 = 144 |
| F3 = 2 | F13 = 233 |
| F4 = 3 | F14 = 377 |
| F5 = 5 | F15 = 610 |
| F6 = 8 | F16 = 987 |
| F7 = 13 | F17 = 1597 |
| F8 = 21 | F18 = 2584 |
| F9 = 34 | F19 = 4181 |
The 100th Fibonacci number is 354224848179261915075 (the first 100 Fibonacci numbers).
Fibonacci Problem
We can generate the Fibonacci Sequence Number in various ways, like using and without the recursion.
Fibonacci Recursion ( Fib Recursion )
In Java programming, exploring the Fibonacci series using recursion, an awesome technique where a function calls itself directly or indirectly, is a methodical approach. The Fibonacci series, renowned for its sequence of numbers where each number is the sum of the two preceding ones, is implemented in Java through a recursive strategy.
This recursive method in Java allows for an elegant and concise representation of the Fibonacci series, leveraging the language’s capability for recursive function calls. By employing recursion in Java, programmers can create a compact and efficient solution for generating the Fibonacci series, showcasing the language’s flexibility in handling mathematical sequences.
package com.softwaretestingo.programsonnumbers;
public class FibonacciSequenceNumbersRecursion
{
static int count=20, n, n1=0,n2=1,n3=0;
public static void main(String[] args)
{
System.out.println("Fibonacci Series Upto " + count + " numbers ");
//printing 0 and 1
System.out.print(n1+" "+n2);
//Because Already 2 Numbers are Printed
printFibonacci(count-2);
}
private static void printFibonacci(int count)
{
if(count>0)
{
n3 = n1 + n2;
n1 = n2;
n2 = n3;
System.out.print(" "+n3);
printFibonacci(count-1);
}
}
}
Output:
Fibonacci Series Upto 20 numbers 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
Fibonacci Numbers without Using Recursion
Finding Fibonacci numbers without using recursion is straightforward. Instead of the traditional recursive method, this approach uses direct, non-repetitive steps to compute Fibonacci numbers efficiently. By avoiding recursion, we simplify the process, making it more accessible and less resource-intensive.
This alternative method provides a practical solution for those seeking a direct route to generate Fibonacci numbers without the details associated with recursive algorithms. It’s about finding a simpler, more direct path to unveil the sequence without relying on repetitive steps.
package com.softwaretestingo.programsonnumbers;
public class FibonacciSequenceNumbersWithoutRecursion
{
public static void main(String[] args)
{
int n = 10, firstTerm = 0, secondTerm = 1;
System.out.println("Fibonacci Series till " + n + " terms:");
for (int i = 1; i <= n; ++i)
{
System.out.print(firstTerm + " ");
// compute the next term
int nextTerm = firstTerm + secondTerm;
firstTerm = secondTerm;
secondTerm = nextTerm;
}
}
}
Output:
Fibonacci Series till 10 terms: 0 1 1 2 3 5 8 13 21 34
Fibonacci Numbers Using While Loop
It would be best to be careful about the condition in the while loop when generating the Fibonacci Series using a while loop. The code below shows how this works in Java.
package com.softwaretestingo.programsonnumbers;
public class FibonacciSequenceNumbersWhileLoop
{
public static void main(String[] args)
{
int i = 1, n = 10, firstTerm = 0, secondTerm = 1;
System.out.println("Fibonacci Series till " + n + " terms:");
while (i <= n)
{
System.out.print(firstTerm + " ");
int nextTerm = firstTerm + secondTerm;
firstTerm = secondTerm;
secondTerm = nextTerm;
i++;
}
}
}
Output:
Fibonacci Series till 10 terms: 0 1 1 2 3 5 8 13 21 34
Display Fibonacci Series Using for Loop
This program will help you to write a Java program that generates the first ‘n’ numbers in the Fibonacci Series using for loops. The logic used here is quite simple. First, initialize the first two numbers of the series.
Then, use a for loop, which adds up its two immediate predecessors and prints out the value. This process continues until your program prints out the first ‘n’ numbers in the series.
package com.softwaretestingo.programsonnumbers;
public class FibonacciSequenceNumbersForLoop
{
public static void main(String[] args)
{
int n = 10, firstTerm = 0, secondTerm = 1;
System.out.println("Fibonacci Series Upto " + n + " Numbers ");
for (int i = 1; i <= n; ++i)
{
System.out.print(firstTerm + " ");
// compute the next term
int nextTerm = firstTerm + secondTerm;
firstTerm = secondTerm;
secondTerm = nextTerm;
}
}
}
Output:
Fibonacci Series Upto 10 Numbers 0 1 1 2 3 5 8 13 21 34
Print Fibonacci Numbers From 1 to 100 Using While Loop
Instead of displaying the Fibonacci series up to a certain number, we display only the series up to that number. So, in this example, we would display the Fibonacci numbers up to 100.
package com.softwaretestingo.programsonnumbers;
public class FibonacciSequenceNumbersUpto100
{
public static void main(String[] args)
{
int n = 100, firstTerm = 0, secondTerm = 1;
System.out.println("Fibonacci Series Upto " + n + ": ");
while (firstTerm <= n)
{
System.out.print(firstTerm + " ");
int nextTerm = firstTerm + secondTerm;
firstTerm = secondTerm;
secondTerm = nextTerm;
}
}
}
Output:
Fibonacci Series Upto 100: 0 1 1 2 3 5 8 13 21 34 55 89
Conclusion:
The Fibonacci Series is a fascinating mathematical concept with wide-ranging applications, from nature to computer science. This exploration has aimed to unravel its beauty and utility, shedding light on its recursive nature and real-world significance.
As we continually enhance our content, we invite you, our readers, to share your insights, comments, or suggestions. Your feedback is invaluable in shaping the quality and clarity of our articles. Feel free to leave a comment below, sharing your thoughts or suggesting areas for improvement. Together, let’s enrich a community of knowledge and learning.
